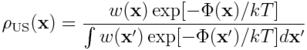Umbrella Sampling (US)
Technika wyznaczania potencjału średnich sił (PMF) stosowana w przypadku, gdy naturalnie zdefiniowany jest pewien parametr porządku (oznaczanym często przez ξ). Aby wyznaczyć PMF potrzebne jest dokładnie przepróbkowanie przestrzeni konfiguracyjnej dla wszystkich wartości ξ, zaś w większości przypadków (m.in. wiązanie ligandu przez enzym), ze względu na występujące w krajobrazie energetycznym bariery, układ będzie występował bardzo rzadko w niektórych rejonach.
US wymusza próbkowanie niekorzystnych energetycznie rejonów ξ, poprzez nałożenie dodatkowego potencjału (często w kształcie paraboli), który wpływa na gęstość prawdopodobieństwa próbkowania. Wówczas, efektywna gęstość prawdopodobieństwa (wynikająca z potencjału układu, Φ, i dodatkowego potencjału) przyjmuje postać krzywej przypominającej swoim kształtem parasol, skąd nazwa metody (ang. umbrella = parasol).
Formalizm
Próbkowanie w Umbrella Samplingu przebiega według poniższej gęstości prawdopodobieństwa:
gdzie w oznacza dodatkowy potencjał, utrzymujący układ w porządanym sąsiedztwie zadanej wartości parametru porządku. Ten dodatkowy potencjał (ang. biasing potential) prowadzi do siły przykładanej zazwyczaj w środku ciężkości układu (bądź podukładu), którego położenie nas interesuje. Jednak w przypadkach, w których interesuje nas nie odległość dwóch obiektów, a bardziej ich orientacja, US stosuje dodatkowy potencjał, który zamiast utrzymywać zadaną odległość, utrzymujący np. stały kąt wyznaczony przez wybrane atomy.
Metoda US polega na przeprowadzeniu szeregu sumulacji, dla wybranych wartości parametru porządku - tzw. wartości centralnych - wokół których dodatkowy potencjał będzie utrzymywał nasz (pod)układ. Po przeprowadzonych symulacjach otrzymujemy histogramy zliczeń w funkcji ξ. Aby przejść do scalania wyników (czyli do wyrugowania dodatkowego potencjału i wyliczania PMFa) należy uzyskać histogramy, które nakładają się na siebie dla sąsiadujących wartości centralnych.
Do wygenerowania PMFa wykorzystuje się albo metodę WHAM, albo nowsze podejście o nazwie MBAR (Multistate Bennett Acceptance Ratio), które gwarantuje profil o najmniejszej wariancji. W obydwu przypadkach potrzebne są trzy zestawy danych:
- Histogramy zliczeń w funkcji ξ dla wszystkich symulacji wykonanych dla różnych wartości centralnych.
- Wartości energii całego układu w poszczególnych krokach dla wszystkich wykonanych symulacji.
- Odchylenia od wartości centralnych w poszczególnych krokach dla wszystkich wykonanych symulacji.
Należy raz jeszcze podkreślić, że jeśli histogramy zliczeń dla symulacji wykonanych dla sąsiednich wartości centralnych nie nakładają się, to niezależnie od metody (WHAM, MBAR) nie uzyskamy wiarygodnego profilu PMF.
Literatura
- Nonphysical sampling distributions in Monte Carlo free energy estimation: Umbrella sampling, J. Comput. Phys. (1977), 23, 187--199, G.M. Torrie, J.P. Valleau.