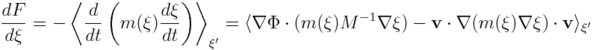(→Adaptive Biasing Force (ABF)) |
(→Formalizm) |
||
| (Nie pokazano 5 pośrednich wersji utworzonych przez tego samego użytkownika) | |||
| Linia 1: | Linia 1: | ||
| + | =Adaptive Biasing Force= | ||
| + | Jedna z nowszych metod wyznaczania różnic energii swobodnej, a konretniej - potencjału średnich sił (PMF), z którego można wyznaczyć różnice energii swobodnej między stanami meta-stabilnymi. Jej główną zaletą jest uniwersalność; do działania wymaga definicji współrzędnej reakcji ξ('''x'''), będącej funkcją konfiguracji układu. Ponadto, ABF jest nieczuły na problemy związane z przeszukiwaniem przestrzeni konfiguracyjnej (utykanie w lokalnych minimach, eksploracja licznych minimów). Do wad należy zaliczyć skomplikowany formalizm i nieintuicyjność, co utrudnia debugowanie. | ||
| + | |||
| + | ==Formalizm== | ||
| + | |||
| + | Wyprowadzenie metody ABF znaleźć można w [1]. Co ciekawe, ABF uznawany jest przez jego twórców za odmianę całkowania termodynamicznego ([[Thermodynamic Integration (TI)|TI]]), pomimo znaczących różnic w podstawowych założeniach (w TI współrzędna reakcji jest niezależnym parametrem, zaś w ABFie jest to funkcja konfiguracji). Jednak idea stojąca za wyprowadzeniem jest ta sama - zarówno ABF jak i TI docelowo generują PMFa. Inne źródła zaliczają ABF do klasy metod o nazwie [[Metadynamika|metadynamika]]. | ||
| + | |||
| + | Ponieważ wyprowadzenie jest dość złożone matematycznie, ograniczymy się w tym artykule jedynie do zapostulowania podstawowej formuły, z której ABF czerpie: | ||
| + | [[Image:Eqn1218.png|thumb|center|x50px]] | ||
| + | gdzie ''M'' oznacza diagonalną macierz mas atomów, '''v''' to prędkości atomów, Φ to potencjał układu, zaś ''m''(ξ) to wielkość skalarna mierząca, bezwładność układu, gdyby rozważać ruch układu wzdłuż współrzędnej reakcji jako ruch ciała punktowego. | ||
| + | Nawiasy kątowe oznaczają warunkową wartość oczekiwaną, przy ustalonej wartości ξ' współrzędnej reakcji. | ||
| + | |||
| + | Zwrócić należy uwagę na dwa aspekty algorytmu ABF, które wynikają z powyższego wzoru. Po pierwsze, jest to wyrażenie na pochodną energii swobodnej względem współrzędnej reakcji w punkcie ξ'. Oznacza to, że gdybyśmy umieli wyliczyć z symulacji wielkość po prawej stronie tej równości, moglibyśmy pokuścić się o scałkowanie tego wyrażenia, co dałoby nam F(ξ), czyli PMF. Jednak wyznaczanie warunkowej wartości oczekiwanej z symulacji jest nieefektywne ze względu na błędy statystyczne, wynikające z zubożonego próbkowania przestrzeni konfiguracyjnej (ustalenie wartości współrzędnej reakcji jest zbyt mocnym ograniczeniem mobilności układu). Z tego względu, w ABFie stosuje się dużo lepszą technikę całkowania, która jest zarazem dużo bardziej skomplikowana (szczegóły znaleźć można w [1,2]). | ||
| + | |||
| + | Po drugie, na podstawie powyższego wzoru w danym kroku symulacji jesteśmy w stanie oszacować, w którą stronę (wzdłuż współrzędnej reakcji) nasz układ będzie postępował. Onacza to, że możemy dołożyć do układu siłę skierowaną przeciwnie, co pozwoli na łatwiejsze przechodzenie układu przez bariery energii swobodnej, zwiększając skuteczność próbkowania. Metoda ABF następnie uwzględnia wpływ tych dodatkowych sił, nie zaburzając obliczania zmian energii swobodnej. | ||
| + | |||
| + | Oznacza to, że ABF jest zarówno algorytmem wyznaczającym energię sobodną (poprzez całkowanie powyższego równania), ale też i metodą próbkowania przestrzeni konfiguracyjnej (co pozwala znajdować stany meta-stabilne układu i potencjalne ścieżki przejść). W celu zaznajomienia się z metodą ABF i szybkiego jej zastosowania w praktyce zachęcamy do zapoznania się ze specjalistycznym szkoleniem w środowisku NAMD (http://www.ks.uiuc.edu/Training/Tutorials/namd/PLB/tutorial-protein-ligand.pdf) oraz doskonałą publikacją [2]. | ||
| + | |||
| + | ==Literatura== | ||
| + | # ''Free energy calculations.'' Springer-Verlag Berlin Heidelberg (2007), C. Chipot , A. Pohorille. | ||
| + | # ''The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask.'' The Journal of Physical Chemistry B 119.3 (2014) 1129--1151, J. Comer, et al. | ||
Aktualna wersja na dzień 12:37, 12 mar 2015
Adaptive Biasing Force
Jedna z nowszych metod wyznaczania różnic energii swobodnej, a konretniej - potencjału średnich sił (PMF), z którego można wyznaczyć różnice energii swobodnej między stanami meta-stabilnymi. Jej główną zaletą jest uniwersalność; do działania wymaga definicji współrzędnej reakcji ξ(x), będącej funkcją konfiguracji układu. Ponadto, ABF jest nieczuły na problemy związane z przeszukiwaniem przestrzeni konfiguracyjnej (utykanie w lokalnych minimach, eksploracja licznych minimów). Do wad należy zaliczyć skomplikowany formalizm i nieintuicyjność, co utrudnia debugowanie.
Formalizm
Wyprowadzenie metody ABF znaleźć można w [1]. Co ciekawe, ABF uznawany jest przez jego twórców za odmianę całkowania termodynamicznego (TI), pomimo znaczących różnic w podstawowych założeniach (w TI współrzędna reakcji jest niezależnym parametrem, zaś w ABFie jest to funkcja konfiguracji). Jednak idea stojąca za wyprowadzeniem jest ta sama - zarówno ABF jak i TI docelowo generują PMFa. Inne źródła zaliczają ABF do klasy metod o nazwie metadynamika.
Ponieważ wyprowadzenie jest dość złożone matematycznie, ograniczymy się w tym artykule jedynie do zapostulowania podstawowej formuły, z której ABF czerpie:
gdzie M oznacza diagonalną macierz mas atomów, v to prędkości atomów, Φ to potencjał układu, zaś m(ξ) to wielkość skalarna mierząca, bezwładność układu, gdyby rozważać ruch układu wzdłuż współrzędnej reakcji jako ruch ciała punktowego. Nawiasy kątowe oznaczają warunkową wartość oczekiwaną, przy ustalonej wartości ξ' współrzędnej reakcji.
Zwrócić należy uwagę na dwa aspekty algorytmu ABF, które wynikają z powyższego wzoru. Po pierwsze, jest to wyrażenie na pochodną energii swobodnej względem współrzędnej reakcji w punkcie ξ'. Oznacza to, że gdybyśmy umieli wyliczyć z symulacji wielkość po prawej stronie tej równości, moglibyśmy pokuścić się o scałkowanie tego wyrażenia, co dałoby nam F(ξ), czyli PMF. Jednak wyznaczanie warunkowej wartości oczekiwanej z symulacji jest nieefektywne ze względu na błędy statystyczne, wynikające z zubożonego próbkowania przestrzeni konfiguracyjnej (ustalenie wartości współrzędnej reakcji jest zbyt mocnym ograniczeniem mobilności układu). Z tego względu, w ABFie stosuje się dużo lepszą technikę całkowania, która jest zarazem dużo bardziej skomplikowana (szczegóły znaleźć można w [1,2]).
Po drugie, na podstawie powyższego wzoru w danym kroku symulacji jesteśmy w stanie oszacować, w którą stronę (wzdłuż współrzędnej reakcji) nasz układ będzie postępował. Onacza to, że możemy dołożyć do układu siłę skierowaną przeciwnie, co pozwoli na łatwiejsze przechodzenie układu przez bariery energii swobodnej, zwiększając skuteczność próbkowania. Metoda ABF następnie uwzględnia wpływ tych dodatkowych sił, nie zaburzając obliczania zmian energii swobodnej.
Oznacza to, że ABF jest zarówno algorytmem wyznaczającym energię sobodną (poprzez całkowanie powyższego równania), ale też i metodą próbkowania przestrzeni konfiguracyjnej (co pozwala znajdować stany meta-stabilne układu i potencjalne ścieżki przejść). W celu zaznajomienia się z metodą ABF i szybkiego jej zastosowania w praktyce zachęcamy do zapoznania się ze specjalistycznym szkoleniem w środowisku NAMD (http://www.ks.uiuc.edu/Training/Tutorials/namd/PLB/tutorial-protein-ligand.pdf) oraz doskonałą publikacją [2].
Literatura
- Free energy calculations. Springer-Verlag Berlin Heidelberg (2007), C. Chipot , A. Pohorille.
- The Adaptive Biasing Force Method: Everything You Always Wanted To Know but Were Afraid To Ask. The Journal of Physical Chemistry B 119.3 (2014) 1129--1151, J. Comer, et al.