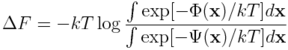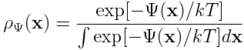(→Free Energy Perturbation (FEP)) |
|||
| Linia 2: | Linia 2: | ||
FEP jest jedną z najstarszych ogólnych metod wyznaczania różnic energii swobodnej między układami o zbliżonych właściwościach (np. enzym związany z ligandem X oraz enzym związany z ligandem Y). | FEP jest jedną z najstarszych ogólnych metod wyznaczania różnic energii swobodnej między układami o zbliżonych właściwościach (np. enzym związany z ligandem X oraz enzym związany z ligandem Y). | ||
W pierwszych zastosowaniach FEP wykorzystywano do względnie prostych układów (np. przy wyznaczaniu energii swobodnej solwatacji jonów), ale jest stosowana do dziś nawet w przypadku najbardziej wymagających problemów (wiązanie białko-ligand, przejścia między stanami). | W pierwszych zastosowaniach FEP wykorzystywano do względnie prostych układów (np. przy wyznaczaniu energii swobodnej solwatacji jonów), ale jest stosowana do dziś nawet w przypadku najbardziej wymagających problemów (wiązanie białko-ligand, przejścia między stanami). | ||
| + | |||
| + | Jednym z najbardziej znanych rozszerzeń Free Energy Perturbation jest całkowanie termodynamiczne ([[Thermodynamic Integration (TI) |thermodynamic integration]]). | ||
==Formalizm== | ==Formalizm== | ||
| + | Przyjmijmy, że jesteśmy zainteresowani różnicą energii swobodnej między układem opisanym potencjałem Φ i układem opisanym przez potencjał Ψ: | ||
| + | [[Image:DeltaFfep.png|thumb|center |x50px]] | ||
| + | Założenie FEP jest następujące: jeżeli potencjały są podobne, tzn. | ||
| + | [[Image:Phi.png|thumb|center |x40px]] | ||
| + | gdzie δ przyjmuje niskie wartości, to możemy oszacować różnicę energii swobodnej, przeprowadzając symulację zgodnie z potencjałem Ψ, tzn. próbkując rozkład: | ||
| + | [[Image:RhoPsi.png|thumb|center|x50px]] | ||
| + | Dla każdej wyprodukowanej konfiguracji '''x''' obliczamy różnicę energii potencjalnych δ('''x'''). | ||
| + | Różnica energii swobodnej wyraża się wówczas następującym wzorem: | ||
| + | [[Image:Eqn9177.png|thumb|center|x40px]] | ||
| + | Założenie o niskich wartościach δ jest istotne - w przeciwnym wypadku aproksymowanie różnic energii swobodnej skazane jest na bardzo wysoki bład statystyczny (przekraczający estymowane wartości). Niestety, założenie to nie jest spełnialne, poza szczególnymi przypadkami, a bez dodatkowych technik FEP nie będzie prowadzić do wiarygodnych wyników. | ||
| − | + | ==Zastosowania== | |
| − | + | Na gruncie Free Energy Perturbation wyrosła matoda [[Thermodynamic Integration (TI)|całkowanie termodynamiczne]], jedna z najbardziej znanych metod wyznaczania różnic energii swobodnej między układami o zbliżonych strukturach. Przyczyna, dla której TI uważa się za niezależną metodę jest to, że od czasu pierwszego sformułowania FEP wprowadzono liczne techniczne poprawki dedykowane wyłącznie całkowaniu termodynamicznemu. | |
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
==Literatura== | ==Literatura== | ||
Wersja z 10:58, 6 mar 2015
Free Energy Perturbation (FEP)
FEP jest jedną z najstarszych ogólnych metod wyznaczania różnic energii swobodnej między układami o zbliżonych właściwościach (np. enzym związany z ligandem X oraz enzym związany z ligandem Y). W pierwszych zastosowaniach FEP wykorzystywano do względnie prostych układów (np. przy wyznaczaniu energii swobodnej solwatacji jonów), ale jest stosowana do dziś nawet w przypadku najbardziej wymagających problemów (wiązanie białko-ligand, przejścia między stanami).
Jednym z najbardziej znanych rozszerzeń Free Energy Perturbation jest całkowanie termodynamiczne (thermodynamic integration).
Formalizm
Przyjmijmy, że jesteśmy zainteresowani różnicą energii swobodnej między układem opisanym potencjałem Φ i układem opisanym przez potencjał Ψ:
Założenie FEP jest następujące: jeżeli potencjały są podobne, tzn.
gdzie δ przyjmuje niskie wartości, to możemy oszacować różnicę energii swobodnej, przeprowadzając symulację zgodnie z potencjałem Ψ, tzn. próbkując rozkład:
Dla każdej wyprodukowanej konfiguracji x obliczamy różnicę energii potencjalnych δ(x). Różnica energii swobodnej wyraża się wówczas następującym wzorem:
Założenie o niskich wartościach δ jest istotne - w przeciwnym wypadku aproksymowanie różnic energii swobodnej skazane jest na bardzo wysoki bład statystyczny (przekraczający estymowane wartości). Niestety, założenie to nie jest spełnialne, poza szczególnymi przypadkami, a bez dodatkowych technik FEP nie będzie prowadzić do wiarygodnych wyników.
Zastosowania
Na gruncie Free Energy Perturbation wyrosła matoda całkowanie termodynamiczne, jedna z najbardziej znanych metod wyznaczania różnic energii swobodnej między układami o zbliżonych strukturach. Przyczyna, dla której TI uważa się za niezależną metodę jest to, że od czasu pierwszego sformułowania FEP wprowadzono liczne techniczne poprawki dedykowane wyłącznie całkowaniu termodynamicznemu.