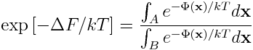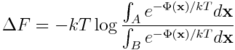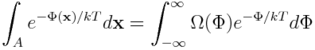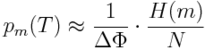Spis treści
WHAM
Wighted Histogram Analysis Method (WHAM) jest jedną z powszechnie stosowanych metod wyznaczania energii swobodnej, stosowana (w różnych formach) do dziś. Zaproponowana została przez Ferrenberga i Swendsena w 1989 [1] do ogólnego zastosowania, a zaadaptowana przez Kumara i Rosenberga do świata biomolekuł w 1992 roku [2].
Wprowadzenie
Przypomnijmy, że różnica energii swobodnej stanów A oraz B wyraża się wzorem (zobacz tu):
bądź równoważnie:
gdzie Φ oznacza funkcję położeń atomów układu x, wyznaczającą energię potencjalną układu.
Zauważ, że stany A i B to w istocie podzbiory przestrzeni konfiguracyjnej, tzn.
gdzie N oznacza liczbę atomów układu (np. białko+ligand+jony+solwent+...). Przestrzeń konfiguracyjna pełna jest "nierealnych" obszarów, czy też: niefizycznych tzn. takich, którym odpowiada bardzo wysoka energia potencjalna. Przyczyną mogą być zawady steryczne, bądź nienaturalnie długie wiązania między atomami. Intuicyjnie, takie niefizyczne obszary nie powinny wpływać na prawdopodobieństwo danego stanu, a zatem - również na energię swobodną. Istotnie, wkłady pochodzące z tych wysoko-energetycznych konfiguracji są pomijalne w całkach w powyższych wzorach (energia potencjalna jest w wykładniku e z ujemnym znakiem).
Jest też jasne, że nisko-energetyczne konfiguracje będą miały istotny wpływ na różnicę energii swobodnej, pomimo tego, że jest ich stosunkowo niewiele. Natomiast trudno antycypować na podstawie samych wzorów, że znaczący wkład do energii swobodnej mają obszary o "średniej" energii potencjalnej. Wprawdzie przyczynki do energii swobodnej wykładniczo maleją z rosnącą energią potencjalną, obszarów o "nie najniższej" energii potencjalnej są olbrzymie.
Algorytm WHAM iteracyjnie estymuje obszary o zadanych wartościach energii potencjalnej, co pozwala obliczyć całki występujące we wzorach na energię swobodną. Jej podstawową wadą jest to, że pozwala wyznaczyć jedynie różnice energii swobodnej (a zatem ilorazy całek), a nie wartości bezwzględne.
Formalizm
Algorytm WHAM opiera się na estymowaniu całek występujących w energii swobodnej poprzez całkowanie ich po zmiennej Φ, tzn. po wartościach energii potencjalnej:
występująca we wzorze funkcja Ω(Φ) jest gęstością stanów o energii potencjalnej równej Φ. Gęstość stanów ma wiele ciekawych własności, ale wspomnimy tu tylko o jednej, istotnej z punktu widzenia WHAMa: nie zależy od temperatury. Oznacza to, że do estymowania Ω(Φ) możemy posłużyć się danymi uzyskanymi z kilku symulacji, wykonanych w różnych temperaturach. To ważne, ponieważ w wysokich temperaturach (rzędu 600 K) konfiguracje o "średnich" wartościach energii potencjalnej są chętniej odwiedzane, niż w symulacjach przeprowadzonych w niższych (rzędu 300 K) temperaturach.
Podejście zastosowane w WHAM polega na połączeniu prawdopodobieństwa znalezienia układu w konfiguracji o zadanej energii potencjalnej:
z gromadzonymi w histogramie wystąpieniami tych konfiguracji w symulacji:
gdzie ΔΦ jest szerokością binu w histogramie, H(m) jest liczbą zliczeń konfiguracji o m-tej wartości energii potencjalnej, zaś N jest całkowitą liczbą zliczeń (kroków symulacji).
Literatura
- Optimized Monte Carlo Data Analysis. Phys. Rev. Lett. (1989) 63, 1195--1198, A. M. Ferrenberg, R. H. Swendsen.
- The weighted histogram analysis method for free‐energy calculations on biomolecules. I. The method. Journal of computational chemistry 13.8 (1992): 1011-1021, S. Kumar, J. M. Rosenberg.